Vergleich zweier verbreiteter Vorgehensweisen
Maßgebend für die Ausgestaltung einer Unterrichtsreihe ist oftmals jene aus dem verwendeten Schulbuch, denn – so die Annahme – dabei handle es sich um erprobtes Material und in der Praxis ist es für Lehrer schon aus Gründen der Zeitökonomie nur eingeschränkt ratsam, die didaktische Aufbereitung eines Themas von Null beginnend neu auszugestalten. Warum auch das Rad wieder und wieder neu erfinden?
Im Folgenden soll daher beispielhaft gezeigt werden, welche Wege bei der Vermittlung der Bruchrechnung in etablierten Lehrwerken eingeschlagen werden und welche Konsequenzen dies für den Lernerfolg der Schüler haben kann.
Konkret möchte ich den Lambacher Schweizer (aus dem Klett-Verlag) mit der Reihe Neue Wege (vom Westermann-Verlag) miteinander kontrastieren. Hier nun die Sequenzierung der entsprechenden Teilthemen in diesen Schulbüchern.
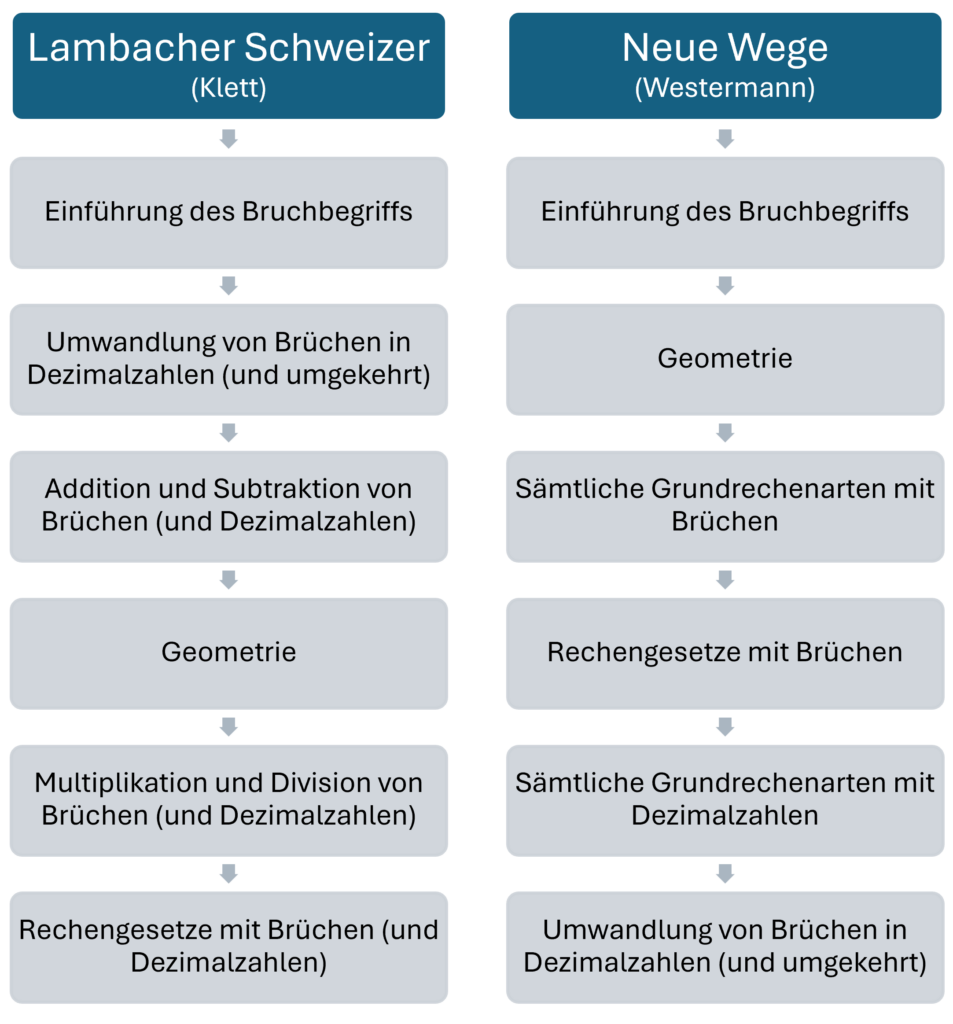
Neben einigen offenkundigen Gemeinsamkeiten, gibt es bedeutsame Unterschiede bei der Reihenfolge der abgehandelten Themen. Beides wird im Folgenden beleuchtet.
Einführung des Bruchbegriffs
Selbstverständlich werden in beiden Lehrwerken die Grundlagen mit passender Nähe zu den Alltagserfahrungen der Schüler gelegt, wobei kein Weg an zerteilten Pizzen vorbeiführt. Davon ausgehend wird das Erweitern und Kürzen von Brüchen eingeführt und die Prozentschreibweise als eine besonders zweckmäßige Bruchdarstellung erläutert.
Es gibt hierbei nur einen maßgeblichen Unterschied: Bei den Neuen Wegen werden – bereits zum Ende der fünften Klasse – im Rahmen der Teilbarkeitsregeln die für die Bruchrechnung so nützlichen Konzepte des ggT und kgV behandelt, wohingegen diese beim Lambacher Schweizer in einen optionalen und sehr knapp gehaltenen Exkurs ausgelagert werden.
Insbesondere das kleinste gemeinsame Vielfache ist für das Auffinden des Hauptnenners bei der Addition oder Subtraktion ungleichnamiger Brüche von Relevanz, so dass ein frühzeitiges Einüben dieser Rechentechnik eine willkommene Vorentlastung bietet.
Geometrie-Einschub
Der Geometrie-Einschub wirkt auf den ersten Blick wie eine Ablenkung, erfüllt aber zugleich mehrere wichtige Funktionen: Zum einen bringt er Abwechslung ins Unterrichtsgeschehen, was aus motivationaler Sicht stets begrüßenswert ist – gerade bei sehr umfangreichen Themen wie der Bruchrechnung -, zum anderen bietet er die Möglichkeit, die erworbenen Grundkenntnisse ein wenig „sacken“ zu lassen. Diese spiralcurriculare Vorgehensweise, bei der nach einer Pause und dem damit unausweichlichen teilweise Vergessen des Stoffes eine Auffrischung erfolgt, folgt dem Prinzip des Spaced Practice, des zeitlich verteilten Üben, dessen Lernwirksamkeit kognitionspsychologisch wohlbelegt ist.
Grundrechenarten der Bruchrechnung
Während der Lambacher Schweizer zunächst nur Addition und Subtraktion von Brüchen behandelt und Multiplikation sowie Division auf ein späteres Kapitel verschiebt, werden bei den Neuen Wegen sämtliche Grundrechenarten im Block abgearbeitet. Da einer der Hauptschwierigkeiten der Schüler in der Unterscheidung besteht, wann bei zwei vorliegenden Brüchen diese auf einen gemeinsamen Nenner gebracht und wann Zähler sowie Nenner jeweils getrennt voneinander behandelt werden dürfen, ist letzteres Vorgehen entschieden sinnvoller.
In diesem Zusammenhang darf nicht der Hinweis das Prinzip des sogenannten Interleaved Practice (Vermischtes Üben) fehlen, bei der bewusst ähnlich aussehende Aufgaben vermischt werden, so dass die Schüler stets von Neuem überlegen müssen, welche Herangehensweise die jeweils zielführende ist. Die Wirksamkeit dieses Verfahrens ist gut untersucht; eine lesenswerte Studie zu diesem Thema ist beispielsweise der Artikel „Interleaved Practice Improves Mathematics Learning“ von Doug Rohrer und Kollegen (hier zu finden: https://www.researchgate.net/publication/280326212_Interleaved_Practice_Improves_Mathematics_Learning)
Solche Übungen gibt es dann auch bei den Neuen Wegen – wenn auch deren Umfang aus meiner Sicht hätte größer ausfallen können -, beim Lambacher Schweizer sucht man sie indes vergebens.
Umwandlung von Brüchen ins Dezimalzahlen (und umgekehrt)
Die Erkenntnis, dass Brüche wie Dezimalzahlen gleichermaßen gültige Darstellungen von Zahlen sind, ist von zentraler Bedeutung für die Entwicklung eines robusten Zahlenverständnis und für den Mathematik-Unterricht der Folgejahre auch von praktischer Bedeutung. Wobei nicht wenige Schüler daraus häufig bloß die Schlussfolgerung ziehen, einfach sämtliche Brüche in Dezimalzahlen zu konvertieren, um die nur unzureichend verstandene Bruchrechnung vollständig zu umschiffen (und in der Folge gänzlich zu vergessen).
Der Lambacher Schweizer führt diese Umrechnungsmethoden schon sehr früh ein und wirkt damit geradezu wie eine Einladung, dieser Vermeidungsstrategie zu folgen. Steht ein Acht- oder Neuntklässler mit einer derartigen Einstellung vor einer Gleichung wie 1/6x=2/3 so wird im Heft daraus gerne so etwas wie 0,16x=0,6666 was dann nur noch mit Taschenrechnerhilfe zu lösen ist (wer hier Rundungsfehler findet, darf sie behalten…).
Bei den Neuen Wegen hingegen werden diese Umrechnungsmöglichkeiten erst zum Abschluss vorgestellt, nachdem die Bruchrechnung hoffentlich bereits gefestigt ist.
Fazit
Es sollte klar geworden sein, dass die Pfade durchs Dickicht der Bruchrechnung der beiden Lehrwerke deutlich voneinander abweichen und sich dabei erhebliche qualitative Unterschiede auftun. Und obwohl es sehr offensichtlich ist, wie viel besser in diesem Falle Westermanns Neue Wege abschneiden, bleibt auch bei diesen noch genügend Raum für Verbesserungen, so dass man als Lehrer gut beraten ist, sich bei der Konzeption der eigenen Unterrichtsreihen nicht zu sehr auf das Material der Schulbuchverlage zu verlassen.
